Problem #015
Tags: asymptotic notation
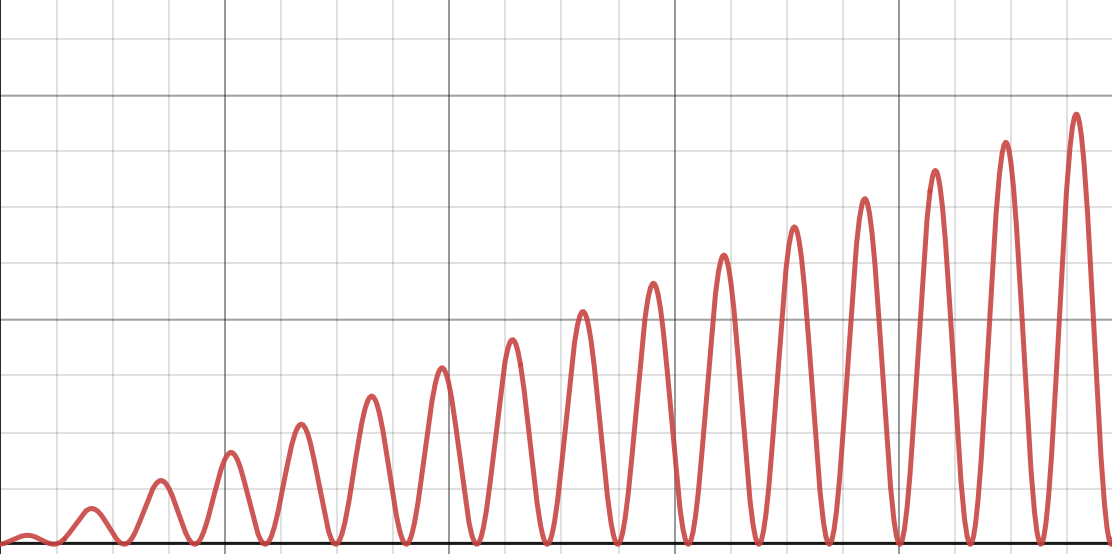
Let \(f(n) = n \cdot(\sin{n} + 1 )\). A plot of this function is shown below.
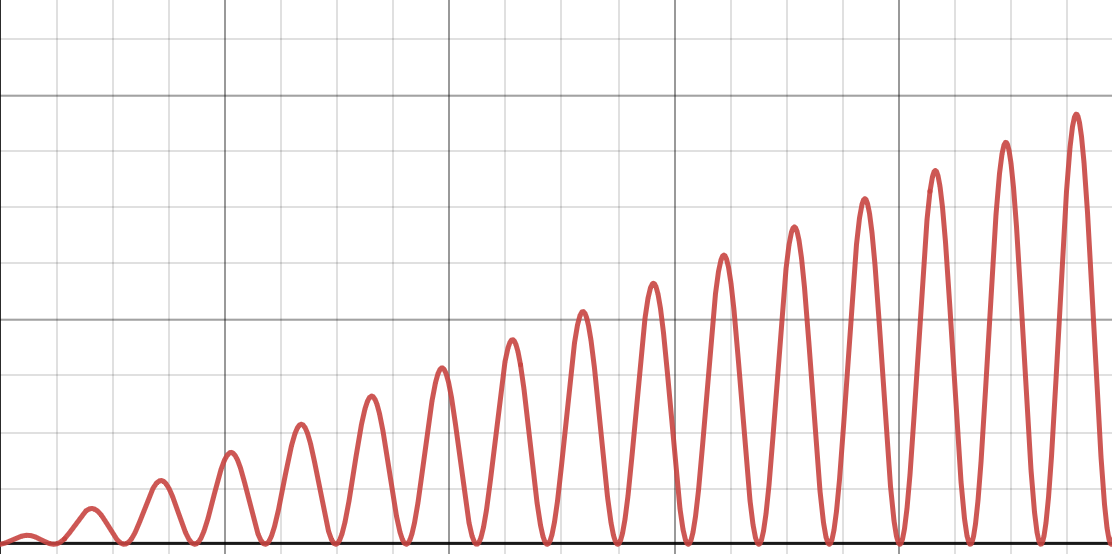
True or False: \(f(n) = \Theta(n)\).
Solution
False.
Remember that for \(f(n)\) to be \(\Theta(n)\), it has to be both upper- and lower-bounded by some positive constant times \(n\). This function is upper bounded by \(O(n)\), but it doesn't have a lower bound of \(\Omega(n)\). Therefore, it can't be \(\Theta(n)\).
In other words, there is no positive constant \(c\) and no positive number \(N\) such that \(f(n) > c n\) for all \(n > N\).
If you had to describe this function in asymptotic notation, you could say that \(f(n) = O(n)\)(and that would be a tight upper bound), but there is no lower bound, since the function keeps coming back down to zero.